We generally define volume as a quantity that is scalar in nature that expresses or represents the magnitude of a three-dimensional region around a surface that is closed. Therefore, the volume of the pyramid can be regarded as the space which the sides of the pyramid have occupied. We can also define the volume of a pyramid as the total number of cubic units it can fill inside it. A pyramid is a kind of polygon known as a polyhedron. There are various types of pyramids classified on the basis of their adjacent side or base such as a square pyramid, rectangular pyramid, triangular pyramid, and so on. In this article, we will try to cover some basic concepts regarding the volume of pyramids and do a detailed analysis of them.
Formula Given for the Volume of a Pyramid
In the paragraph mentioned above, we dealt with the definition of a pyramid along with its volume. In this paragraph, we will try to understand the volume of a pyramid. It can be defined as the space in which the sides of the pyramid have occupied or the total number or cubic units it can fill inside it. Mathematically, the volume of a pyramid is given by, ⅓ * b * h where ‘b’ is defined as the base of the pyramid and ‘h’ is regarded as the height of the pyramid. We already know that there are various types of pyramids. Thus, they might have their own formula according to the area of the base. In order to grasp the concept in a better way, we must solve some calculations based on it. The following examples are mentioned below.
Example 1: Find the volume of a pyramid given that the base of the pyramid is 3 cm and height is 6 cm?
Provided that,
The base of the pyramid = 3 cm
Height of the pyramid = 6 cm
Using the volume of the pyramid = ⅓ * b * h
⅓ * 3 * 6 = 6 cm cubic units.
Therefore, the volume of the pyramid = 6 cm cubic units.
Example 2: Find the volume of a pyramid given that the base of the pyramid is 4 cm and height is 6 cm?
Provided that,
The base of the pyramid = 4 cm
Height of the pyramid = 6 cm
Using the volume of the pyramid = ⅓ * b * h
⅓ * 4 * 6 = 8 cm cubic units.
Therefore, the volume of the pyramid = 8 cm cubic units.
Properties of Pyramid
The following points mentioned below signify the properties of a pyramid:
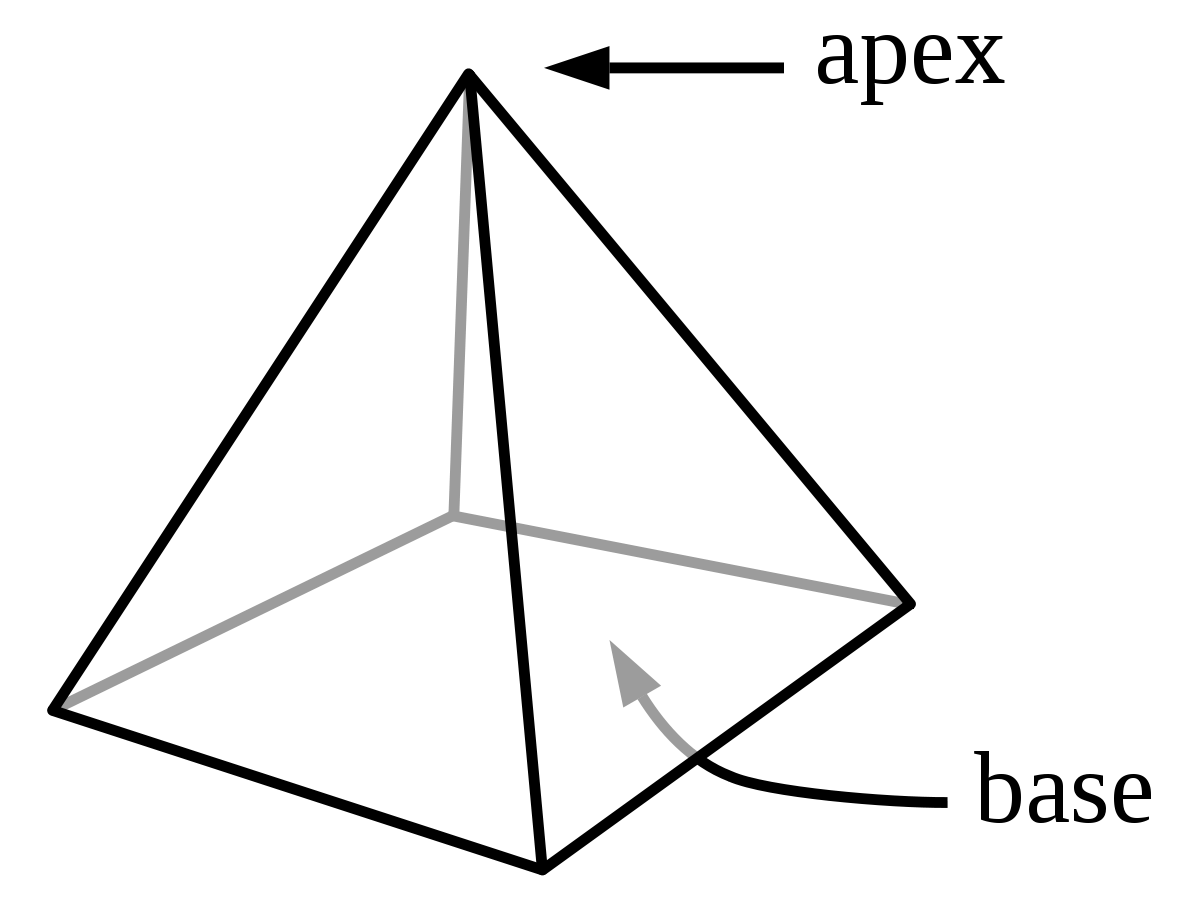
- A pyramid consists of three significant parts such as the face, the apex, and the base.
- The base of the polygon is considered as the shape of a square. The other two sides are known as the lateral faces of the pyramid.
- Whenever the base is in the shape of a regular polygon, then the triangles are defined as congruent and isosceles triangles.
If you want to learn about the volume of the pyramid in a detailed manner, a fun way, and an interactive manner, you may visit the website of Cuemath.
Take Math Classes from Cuemath and Master the Subject of Math
Cuemath is one of the best online platforms for live online classes on math. Concept clarity is of primal importance when we are studying a subject like math. Lack of conceptual clarity is one of the primary reasons why students run away from math and fear it. Here is where the wonderful platform of Cuemath comes to your rescue. It has the best teachers of the subject who focus primarily on making the foundation of students clear in each topic of the subject. Online math classes from Cuemath come at a very affordable rate. You can visit Cuemath’s website if you want to take math classes from the expert teachers who focus on the ‘why’ instead of the ‘what’.